Theory of Light and Color

9. Luminance Properties : Angle of View and Distance
Luminance, as well as illuminance, measures brightness in the space we live in. It is an index of the brightness of the light source or a reflecting surface (wall, ceiling, etc.).
Luminance (radiance) is an important metric for machine vision. We can use luminance to evaluate light sources, especially for bright field applications.
This section describes the key properties of luminance.
Behavior of Light on Reflecting Surfaces
Luminance is a luminous quantity defined by the area and the solid angle. ≪1≫ Thus, light diffusion is important to luminance. In which direction and with what intensity does light diffuse from a light source? Is the surface reflective? How does the reflected light behave? Consider the simplest case where one ray of light is reflected on the surface.
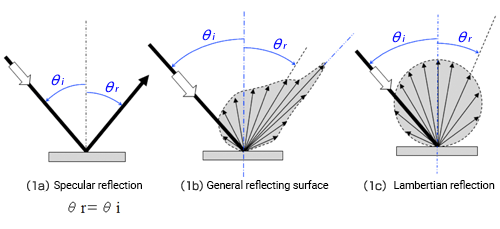
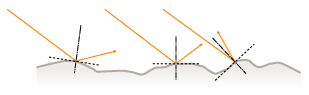
Fig. (1a) illustrates regular reflection, also called specular reflection, which occurs on mirror-like surfaces. A ray of light at the angle of incidence θi reflects at the same angle θi (θr = θi) on the opposite side of the surface normal. The mirror surface will be bright from the angle of regular reflection (θr = θi) but dark from any other direction (θr ≠ θi).
In contrast, a non-glossy surface like white chalk will be bright from any angle. It is a diffuse reflecting surface that reflects light in many directions. The luminous intensity changes with the angle of reflection θr.
Fig. (1c) shows a cross-section of an ideal diffuse reflecting surface, also known as a Lambertian surface. ≪2≫ A Lambertian surface has equal luminance when viewed from any angle. Regardless of θi, the distribution of luminous intensity at θr (Ι(θr)) is spherical. A perfect reflecting diffuser has no absorption and reflects all light.
Fig. (1a) and (1c) above are extreme cases. In general, as shown in Fig. (1b), there is a component of specular behavior (θr = θi), and the remaining light diffuses in many directions. ≪3≫ A surface will be somewhat bright even if it is not viewed from the direction of regular reflection. The glossier the surface, the greater the regular reflection component.
In general, diffuse reflection is a function of both the angle of incidence θi and the angle of reflection θr. This is because angle θr changes with angle θi.
I = I (θi, θr)
The above explains light diffusion on the reflecting surface. Similar light diffusion also occurs in a transparent object. ≪4≫
Light Distribution Characteristics of a Light Source Surface
A light source is not a reflection (transmission) surface. Its surface emits the light by itself. How then does a light source surface diffuse light?
Light distribution characteristics show the direction and luminous intensity/radiant intensity of emitted light from a small area on a light source surface. These characteristics correspond to the diffuse reflection (transmission) property of a reflecting surface. Like reflecting surfaces, light sources can be Lambertian and have the same luminance from any angle of view. ≪5≫
Thus, a surface that reflects/transmits light is in theory a secondary light source. We will treat reflected/transmitted light as a type of light source in the following sections.
Luminance Property 1: Luminance of a Lambertian Surface is Constant from Any Angle of View
Consider a small area A [m2] on a light source surface or reflective surface. If I0 [cd] is the luminous intensity normal to area A, the luminance L0 [cd / m2] in the same direction equals
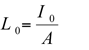
If the luminous intensity at angle θ from the normal is I(θ), the equation for L(θ) becomes
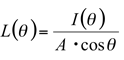
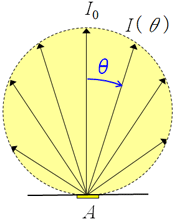
Where A・cos θ indicates the apparent area of A from angle θ. If the luminous intensity of a Lambertian source or surface is
I(θ) = I0・cos θ
The luminance L(θ) at angle θ is
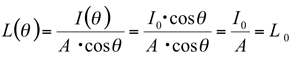
The above shows that the luminous intensity at angle θ becomes darker by cos θ. But the apparent area also becomes narrower by cos θ. Both sides cancel out, and the luminance L(θ) of a Lambertian surface is constant regardless of angle θ.
For example, a fluorescent lamp tube is close to uniform diffuse. Whether you look at the point in front of you or at an oblique angle, both appear to have the same brightness.
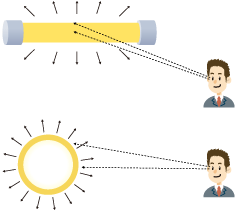
Luminance Property 2: Luminance is Constant from Any Distance
Chapter 8 explained how illuminance becomes darker as distance increases. In contrast, the distance between observer and light source does not affect luminance. For example, the brightness of a TV screen feels the same at 1 m or 3 m. The same is true of a white wall illuminated by a fluorescent lamp.
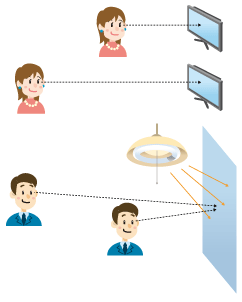
Why does brightness not change when measured as luminance?
You see an object because it forms an image on the retina after passing through the lens of your eye (cornea and lens). You feel brightness by stimulating the photoreceptors on the retina. The amount of stimulus depends on illuminance, the luminous flux incident to a unit area of the retina.
A closer light source (or object) has a larger viewing angle (solid angle ω1). More luminous flux passes through the eye, and the image formed on the retina is also larger.
The farther the distance, the smaller the viewing angle (solid angle ω2). The amount of luminous flux decreases, but the image on the retina also becomes smaller.
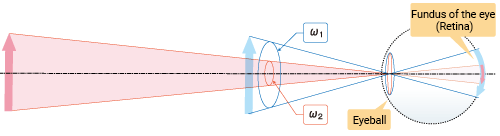
Thus, illuminance remains constant at any distance because the differences in luminous flux and image size offset each other.
The above explanation applies to lighting in general. It is common to treat luminance as a constant regardless of the observation distance. However, there are exceptions to be careful of. ≪6≫
Comment
≪1≫ Definition of luminance
Luminance is the luminous intensity [cd] per apparent unit area [m2]. Luminous intensity is the luminous flux [lm] per unit solid angle [sr]. This makes luminance equal to luminous flux [lm] per apparent unit area [m2] per unit solid angle [sr].
Likewise, radiance is the radiant intensity [W/sr] per apparent unit area [m2], and the radiant intensity is the radiant flux [W] per unit solid angle [sr]. So, radiance is the radiant flux [W] per apparent unit area [m2] per unit solid angle [sr].
≪2≫ Diffuse reflection characteristics of a Lambertian surface
Expressed by the equation,
I(θr) = I0・cosθr
Where I0 is the luminous intensity in the direction normal to the surface (θr = 0°).
≪3≫ Light reflection on the object surface
Objects tend to have intermediate properties between a mirror and chalk. There is a component of specular behavior, but some light will enter the object. The light that enters the object will scatter, change direction, or get absorbed. Some scattered light also travels back out of the surface. From a macroscopic point of view, this scattered light is also reflected light.
The above is the case when the surface of the object is an ideal plane. The actual surface of an object is usually uneven. The angle of regular reflection depends on where the light hits the surface.
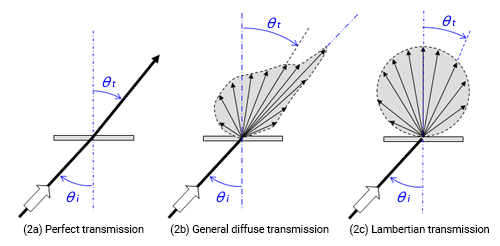
≪4≫ Light diffusion characteristics of a transmission surface
Diffuse transmission occurs when a ray of light transmits through an object.
Consider a ray of light incident to a thin plate at angle θi. If it is a perfect transmissive plate (2a), the light passes straight through it at angle θt (θt = θi). If it is an ideal diffuse plate (2c), the diffusion of the light will be spherical, regardless of the incident angle θi
I (θt) = I0 · cos θt
The diffusion of a semi-transparent plate changes depending on the incident angle (2b).
≪5≫ Lambertian light source
The following equation expresses the luminous intensity I(θ) of a Lambertian source in direction θ with respect to the luminous intensity in the direction normal to the light source (I0):
I ( θ ) = I0 ・ cos θ
The above is the same as the property of Lambertian reflection in ≪2≫.
≪6≫ Preconditions for luminance to remain constant with variation in distance
Luminance in general does not change with distance, but there are some exceptions. Cases (1) ~ (3) outline several examples:
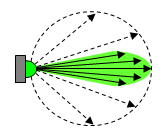
Case (1): The light source surface (or reflecting surface) is not Lambertian
Luminance only remains constant for uniform diffuse surfaces. For example, an LED mounted with a condenser lens or mirror can have very narrow light distribution characteristics. The luminance may change with distance for surfaces that have narrower light distribution.
Case (2): A medium causes significant light absorption and scattering
The medium that light travels through may have strong absorption and scattering properties. This can cause luminous flux to decrease, whether the distance is tens or hundreds of meters. For example, the luminance of a streetlight in fog changes depending on distance. The luminance of light in an aquarium also changes even at a short distance.
Case (3): Extremely short observation distance
Luminous flux and image magnification depend on the angle of view. At extremely short distances, the angle of incidence increases beyond the range of the imaging optical system. This means the luminous flux and the image magnification no longer cancel each other out. As a result, the luminance will change depending on the observation distance.
Radiant Quantities and Luminous Quantities (Part 4)
Luminous intensity / Radiant intensity and Luminance / Radiance

