Theory of Light and Color

8. Illuminance Properties : Distance Dependence and Incident Angle Dependence
As previously discussed, illuminance is the luminous flux incident on a surface per unit area. In machine vision, it is important to remember that the measure of illuminance is highly dependent on the distance and incident angle.
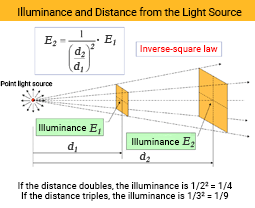
Illuminance vs Distance: The Inverse Square Law of Distance
Illuminance on a flat, highly reflective surface is inversely proportional to the square of the distance from the light source. We know from experience that a surface is brighter when a light source is closer and becomes darker as the light source moves farther away.

Now, imagine a point light source emitting light at solid angles in all directions. The luminous flux is inversely proportional to the square of the distance from the light source. Therefore, the illuminance at a distance twice as far from the light source becomes 1/22 = 1/4 and when the distance is tripled, it becomes 1/32 = 1/9. Conversely, if the distance is 1/2, the illuminance becomes 22 = 4, and if the distance is 1/3, it becomes 32 = 9.
The illuminance on the various planets in our solar system are a good illustration of the inverse-square law. ≪1≫
The law requires a point light source that emits light evenly in all directions. ≪2≫ If the light is not a point source or has variations in intensity depending on the emitting direction, you cannot accurately measure the brightness at a certain distance. ≪3≫ However, the inverse-square law can still be a useful approximation. If the distance is about ten times the diameter of the light source or greater, it is possible to use the inverse-square law as a close estimate.
Illuminance vs. Incident Angle: Lambert's Cosine Law
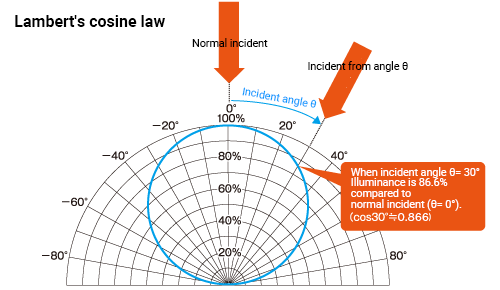
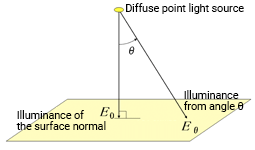
According to Lambert's cosine law, illuminance changes in proportion to the cosine (cos θ) of the incident angle θ to the surface. For a surface illuminated at a certain distance from a light source, the illuminance is highest when the light is perpendicular to the surface (surface normal) and decreases as the incident angle gets further from the surface normal.
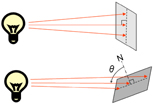
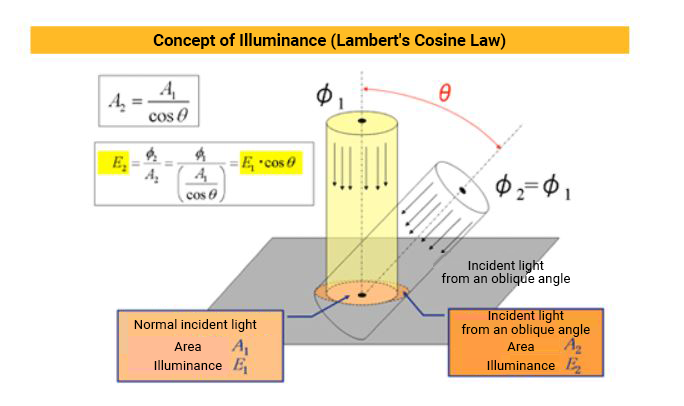
Consider a cylindrical light (luminous flux φ1) that is incident to the surface normal. E1 represents the illuminance if the area illuminated on the surface is A1.

If the cylindrical light irradiates at incident angle θ to the normal, the illuminated surface area would be equivalent to a diagonal cross-section of the cylinder. If the area illuminated on the surface is A2 and the illuminance is E2 (φ2 = φ1 since the luminous flux does not change),
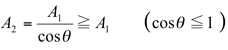
The same amount of light illuminates a broader area, so the illuminance is lower compared to the surface normal. We can calculate illuminance (E2) with the equation
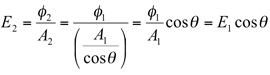
In general terms, the illuminance E2 at incident angle θ to the normal is cos θ times the illuminance of the surface normal (E1). The graph below demonstrates this relationship.
Lambert's cosine law also explains why summer is hot, and winter is cold. ≪4≫
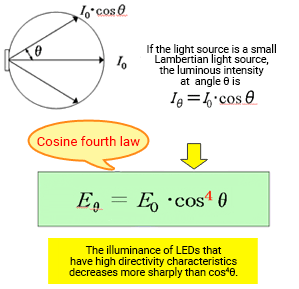
Cosine Fourth Power Law: Illuminance Distribution of a Point Light Source on an Illuminated Surface
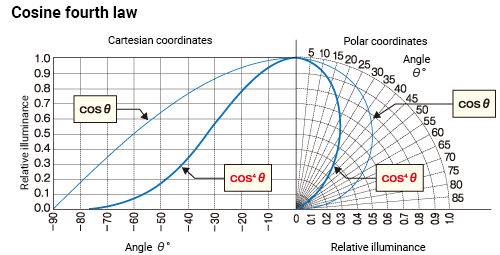
The inverse-square law of distance and Lambert's cosine law can help us understand the cosine fourth power law (cosine fourth law). The cosine fourth law states that for an ideal diffuse point light source, the illuminance Eθ of a surface illuminated from angle θ is cos4 θ times the illuminance of the surface from the normal (E0).
Eθ = E0・cos4 θ ≪5≫
This equation is an important guide for estimating the illuminance distribution when illuminating a flat surface. It shows that illuminance decreases sharply as angle θ increases. For instance, illuminance at a 30° angle is a little over 1/2, and at 45°, it drops to 1/4.
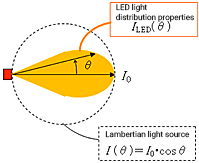
Many types of LEDs such as spot lights have illuminance that decreases more sharply than cos4θ because they have high directivity characteristics. Although light sources can have different light distribution properties, the cosine fourth law is still a useful approximation.
The illuminance properties described in this chapter are determined by geometric conditions. They are not affected by changes in spectral conditions, and irradiance (and sensor-metric illuminance) has the same properties.
Comment
≪1≫ Illuminance during midday on Pluto
Earth is bright during the day due to light from the Sun. The illuminance on Earth varies depending on conditions such as the latitude, time of day, and weather, but the maximum illuminance during midday in Japan on a sunny day is said to be more than 100,000 lx.
How high is illuminance on other planets under the same conditions?
Like Earth, the illuminance on other planets changes depending on the atmosphere, the weather, and other conditions surrounding it. We will ignore these factors and assume there is no atmospheric layer for the sake of this example.
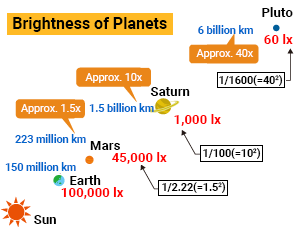
The distance from the Sun to the Earth is about 150 million km with an illuminance of 100,000 lx. The distance from the Sun to Mars is around 223 million km, which is almost 1.5 times the distance from Earth, so the illuminance on Mars is about 100,000 lx × 1/1.52 = 45,000 lx. Similarly, the distance between the Sun and Saturn is about 1.5 billion km, 10 times farther than Earth. Pluto is 6 billion km from the sun, 40 times the distance from Earth. Thus, the illuminance for each is 100,000 lx × 1/102 = 1000 lx for Saturn, and 100,000 lx × 1/402 = 60 lx for Pluto—as bright as the space under a desk.
(Pluto was originally the ninth planet in the solar system since it was discovered in 1930, but in 2006, it was reclassified as a dwarf planet at the General Assembly of the International Astronomical Union.)
≪2≫ How to derive the inverse-square law of distance for illuminance
The inverse-square law of distance for illuminance is theoretically derived from the luminous intensity, the illuminance, and the solid angle.
The luminous intensity (I) is the luminous flux per unit solid angle.
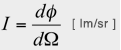
Illuminance is the luminous flux per unit area,
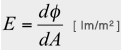
A solid angle is the unit area on a sphere divided by the radius squared of the sphere.
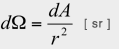
Therefore, from the above three equations

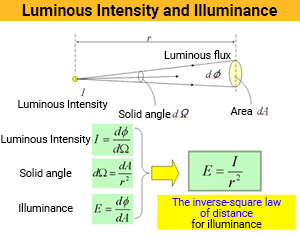
That is to say, illuminance is proportional to the luminous intensity and inversely proportional to the square of the distance if the light source is an ideal diffusive point light source (the area of the light source is infinitely small).
≪3≫ Error in the inverse-square law
Strictly speaking, the inverse-square law only applies to a point light source with diffuse properties. If the light source is relatively larger compared to the distance, there will be a less noticeable change in illuminance even at a distance.
Actual light sources are not point sources, and their light distribution characteristics are not even in all directions. Thus, it is difficult to apply the inverse square law as is.
However, if you divide a certain size light source into many subsections (S1, S2, S3, ---), you can treat each as an individual point light source. Therefore, you can apply the inverse-square law to the luminous flux emitted from each subsection (φ1, φ2, φ3, ---).
The formula to measure the illuminance of this “point source” (unit area A) is
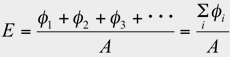
≪4≫ The reason why summer is hot and winter is cold (Northern Hemisphere)
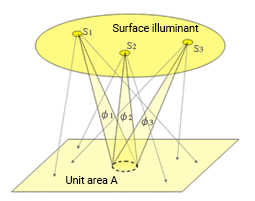
Lambert's cosine law explains why summer is hot and winter is cold in Japan (Northern Hemisphere). Earth revolves around the Sun for a year and the distance between them stays mostly consistent (about 150 million km). Since Earth axial tilt is 23.5° to the normal of the revolution surface, the incident angle of sunlight to the Earth differs in summer and winter when Earth is in opposite positions of its orbit. The incident angle is small in summer (the Sun is high) and large in winter (the Sun is low). Thus, summer is warm because illuminance is high, and it is cold in winter because illuminance is low. (The actual peaks of hot and cold deviate from the summer solstice and the winter solstice by about two months because the specific heat of the Earth causes a time delay.)
≪5≫ Cosine fourth power law
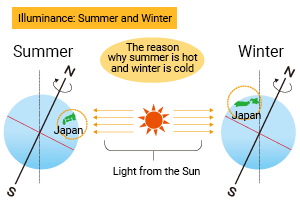
Consider a flat surface at a distance of s0 from a point light source (luminous intensity (I)) that evenly emits light in all directions. Using the inverse-square law, illuminance E0 at the perpendicular incident point P is
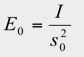
To calculate the illuminance at point Q (projection angle θ from the point light source), imagine a virtual plane passing through Q and facing the point light source. If the distance from the light source to Q is s1 and the illuminance on the virtual plane is E1, then
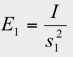
and
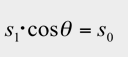
Thus, illuminance E1 on the virtual plane is
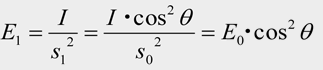
The incident angle to the actual plane is θ since the virtual plane is θ degree to the actual plane. Therefore, the illuminance at Q has to be multiplied by cos θ. Thus, illuminance Eθ becomes
Eθ = E1・cos θ = ( E0・cos2 θ )・cos θ = E0・cos3 θ
The above is the case of the diffusive point light source, which has the luminous intensity (I) emitting the light evenly in all directions. In most practical applications, a light source has a certain area and some degree of directivity.
For the purposes of this proof, we will use the spectral properties of a Lambertian emission surface. A Lambertian emission surface (or reflective surface) has the same luminance from any direction. We will explain in further detail in the next section, Luminance Properties.
When the luminous intensity in the perpendicular direction to the surface (0°) is I0, the luminous intensity (Iθ) in θ direction is
Iθ = I0・cos θ
Therefore, when the plane is illuminated by an evenly diffusive small surface light source, the illuminance at projection angle θ is further multiplied by cos θ and becomes
Eθ = E0・cos4 θ