Theory of Light and Color

7. Radiant Quantities and Luminous Quantities (Part 4)
Luminous Intensity / Radiant Intensity and Luminance / Radiance
In this section, we will talk about directional quantities: luminous and radiant intensity, and luminance and radiance, where the geometric condition is a solid angle. ≪1≫
Geometric Concept of Luminous Intensity and Radiant Intensity
Luminous intensity is a measure of luminous flux (lm) emitted per unit solid angle steradian (sr) from the light source.
Consider our shower example. The showerhead emits water streams at many different angles. As shown in the enlarged view of the shower spray hole, one water stream flows at the angle θ from the normal direction. This water (luminous flux) emitted per unit solid angle in the angle θ direction corresponds to the luminous intensity.
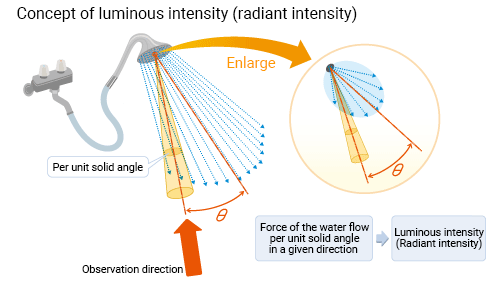
The relationship between luminous flux and luminous intensity is the same as that of radiant flux and radiant intensity, which measures radiant flux (W) emitted per unit solid angle sr (W/sr).
Geometric Concept of Radiance and Luminance
When observing an area of a light source's surface from angle θ, the luminous intensity (cd) per unit area (m2) is called the luminance (cd/m2).
Since luminous intensity (cd) equals (lm/sr), we can express luminance as the luminous intensity per unit solid angle (sr) per apparent unit area from a given direction (cd/m2) = (lm/sr/m2).
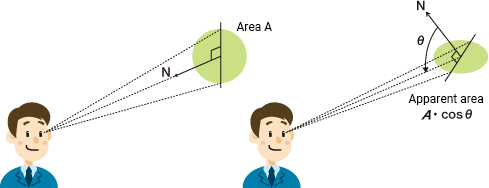
In our shower example, the showerhead emits water streams from its entire surface (area A). Some water streams flow in the direction θ per unit solid angle. An observer at angle θ will only receive these water streams, making the showerhead appear to have a smaller apparent area, expressed as A・cosθ. The luminance is equal to the water streams emitted from that apparent area.
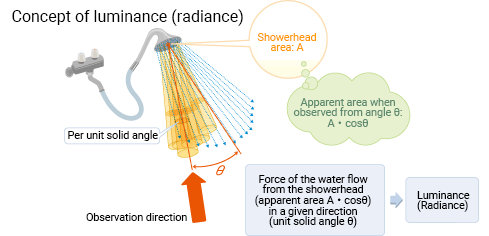
The above describes the relationship between the luminous flux and the luminance (or the luminous intensity and the luminance). We can similarly explain the relationship between the radiant flux and the radiance. The radiant flux (W) emitted per unit solid angle (sr) per apparent unit area (m2) is the radiance (W/sr/m2). Luminance is sometimes a confusing concept but is essentially the visual brightness of a light source or the reflection from a flat, highly reflective surface.
Evaluation of Brightness in Machine Vision: Sensor-Metric Quantities
Until now, we have examined the various types of brightness, divided into luminous and radiant quantities, and defined by different geometric conditions.
However, these quantities are not enough in machine vision because the properties of the machine's eye differ from the standard spectral luminous efficiency V(λ) of the human eye. We need a different quantity of brightness to evaluate radiant quantities (pure physical energy) through the spectral response S(λ) of the machine's eye.
CCS Inc. uses the term sensor-metric quantities to correspond to luminous quantities: sensor-metric flux, quantity of sensor-metric light, sensor-metric illuminance, sensor-metric exitance, sensor-metric intensity, and sensor-metric luminance.
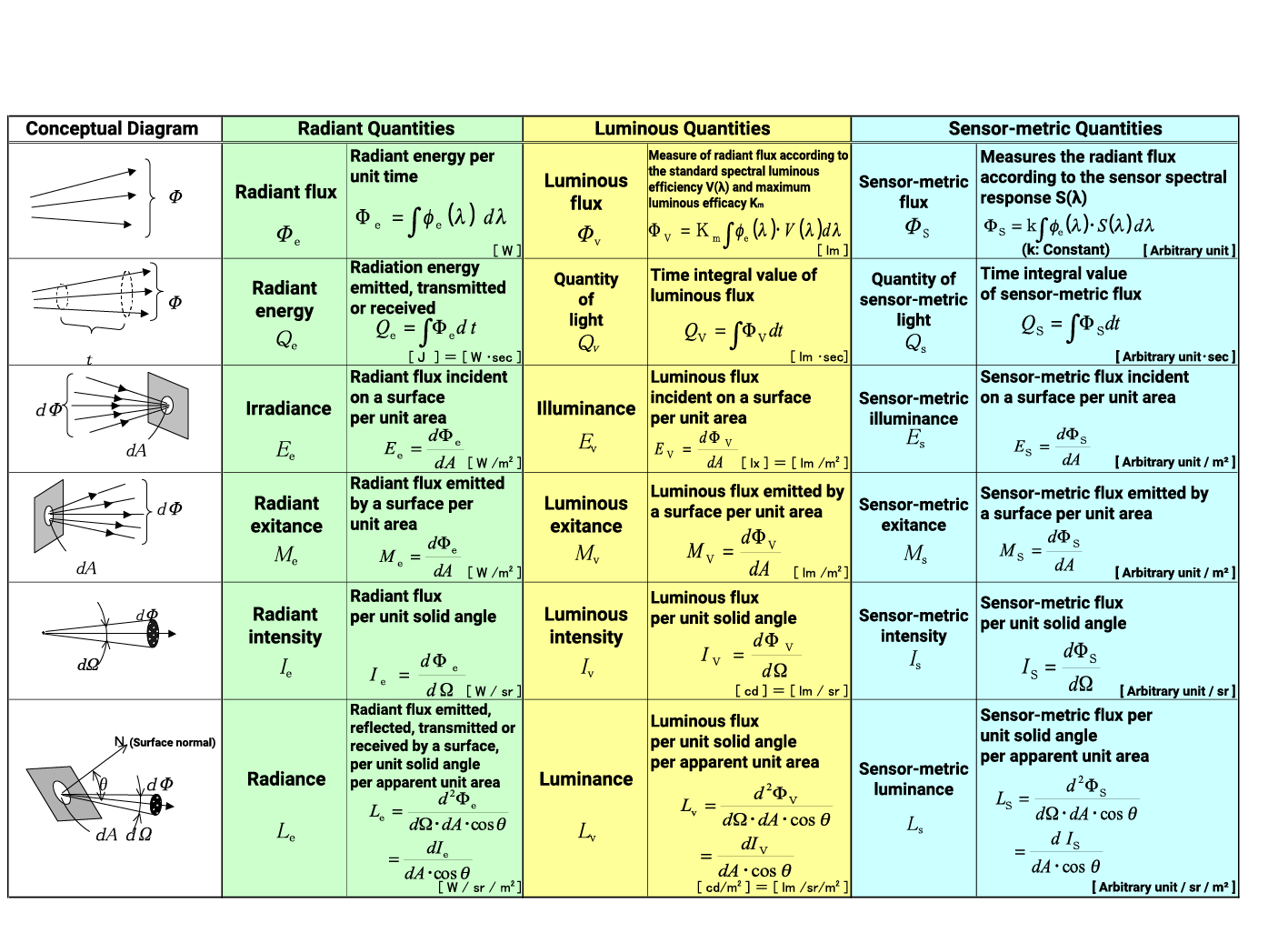
At present, there is no standard definition of the properties of the machine's eye since they vary depending on the purposes. As previously mentioned in chapter 5, we can make relative comparisons between measured values under the same evaluation conditions, but cannot compare the measured values under different conditions. Therefore, we use an arbitrary unit created internally in place of an officially standardized unit of measure. ≪2≫ shows a list of the radiant, the luminous, and the sensor-metric quantities.
Summary
Until now, we have discussed measures of brightness based on electromagnetic radiation (radiant flux (W)) and brightness evaluated by the human eye (luminous flux (lm)). The various radiant and luminous quantities are defined by combining the above with geometric conditions such as area, solid angle, and time.
Next, we will examine illuminance (irradiance, sensor-metric illuminance) versus luminance (radiance, sensor-metric luminance).
Comment
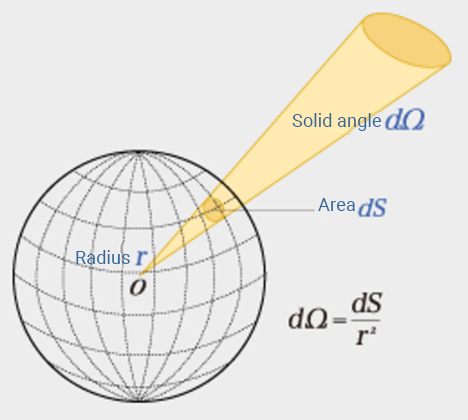
≪1≫ Solid angle
The solid angle extends angles to three-dimensional space.
When measuring plane angles, the most familiar unit degree (°) such as 90° (right angle) and 180° (sum of the interior angle). In addition to degrees, another unit of measure for plane angles is radian (rad).
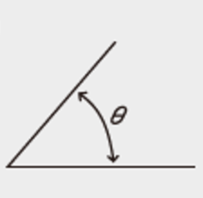
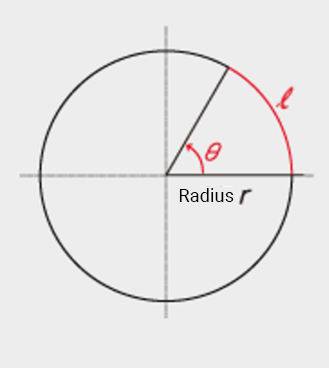
A radian is the central angle θ made by an arc ℓ that is equal in length to radius r. The radian θ is equal to the ratio of the arc length ℓ and the radius r,
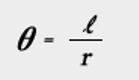
That is, the length of the arc is ℓ = r・θ
The length of the entire circumference ℓ = 2πr, so 360° is expressed as
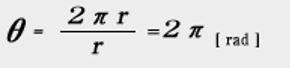
In the same way,
180°= π [rad]
90°= π/ 2 [rad]
In the case of solid angles, the ratio of area dS and radius r of sphere O replaces that of arc length ℓ and radius r. The solid angle dΩ is the area dS of the segment of a sphere from center O.
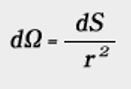
The unit of solid angle is steradian (sr).
≪2≫ Cited reference for radiant quantities, luminous quantities, and sensor-metric quantities
JIS Z 8120:2001 (Optical terminology), JIS Z 8113:1998 (lighting terms)
Radiant Quantities and Luminous Quantities (Part 4)
Luminous intensity / Radiant intensity and Luminance / Radiance

