Theory of Light and Color

15. Color Mixing (Part 1) Additive and Subtractive Color Mixing
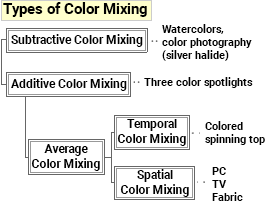
There are three ways to mix color: subtractive, additive, and average color mixing (additive-average color mixing). Color printing, negative photography, and watercolors are all examples of subtractive mixing. Additive color mixing describes color created by coincident light of different colors.
Average color mixing can be either spatial, where colors are too small to distinguish, or temporal, where colors move too fast to distinguish. We will discuss average color mixing in more detail in future chapters.
Three Primary Colors of Additive and Subtractive Color Mixing
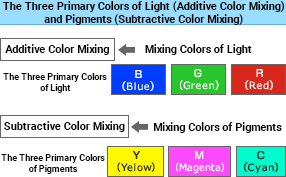
Many people know that you can create various colors by mixing the three primary colors, but these colors differ depending on the type of color mixing.
The three primary colors of additive color mixing are blue (B), green (G), and red (R) and are also known as the three primary colors of light.
The three primary colors of subtractive color mixing are called the three primary colors of pigments: yellow (Y), magenta (M), and cyan (C).
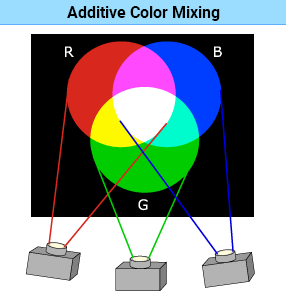
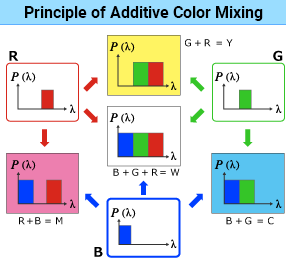
Principle of Additive Color Mixing
In additive color mixing, different colored lights are emitted over the same area, so there is more energy than a monochromatic light.
The figure on the right illustrates additive color mixing. When three projectors emit red (R), green (G), and blue (B) lights respectively onto a black screen, they create new colors when they overlap.
Additive Mixing of Blue (B) and Green (G)
Energy in the short (blue) and medium (green) wavelength ranges stimulates the eye's S-cones and M-cones to the same degree, and we see cyan. (B + G = C)
Additive Mixing of Green (G) and Red (R)
The combined energy in the medium and long (red) wavelength ranges stimulate the M- and L-cones, and the brain perceives yellow. (G + R = Y)
Additive Mixing of Red (R) and Blue (B)
The combination of red and blue light stimulates the L-cones and S-cones and is perceived as magenta. (R + B = M)
Additive Mixing of the Three Primary Colors (B, G, R)
Short, medium, and long wavelengths are present on the area where all three primary colors overlap. The S-, M-, and L-cones receive almost the same degree of stimulus, which the brain perceives as white. (B + G + R = W)
You can create various colors by changing the mixing ratio (irradiance levels) of the three lights.
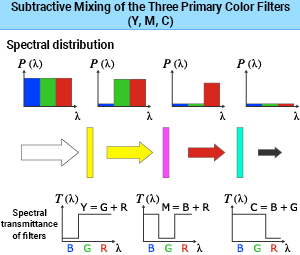
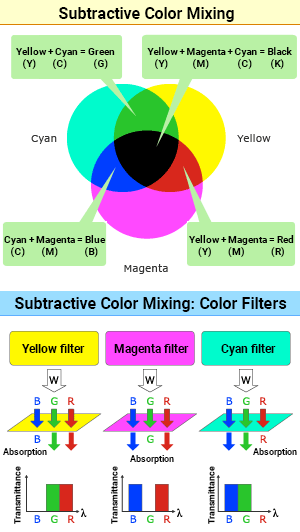
Principle of Subtractive Color Mixing
The diagram on the right of superimposed color filters explains subtractive color mixing.
Equal mixing of yellow (Y) and cyan (C) results in green (G). Similarly, cyan (C) and magenta (M) create blue (B), and magenta (M) and yellow (Y) make red (R). Mixing the three primary colors (Y, M, C) in equal amounts produces black (K).
The spectral transmittance characteristics of the three primary color filters (Y, M, C) illustrate subtractive color mixing (see right).
The yellow filter (Y) absorbs short wavelengths and transmits medium and long wavelengths.
The magenta filter (M) absorbs medium wavelengths and transmits short and long wavelengths.
The cyan filter (C) absorbs long wavelengths and transmits medium and short wavelengths.
Consider what happens to white light (W) when two of these filters are combined:
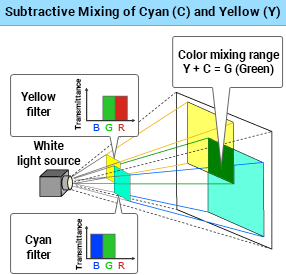
Subtractive Mixing of Cyan (C) and Yellow (Y)
A cyan filter transmits short and medium wavelengths to the yellow filter, which only transmits the medium wavelength range. As a result, the M-cones are stimulated, and the light is green. (C + Y = G)
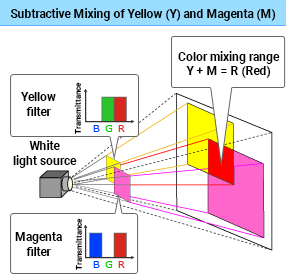
Subtractive Mixing of Yellow (Y) and Magenta (M)
The transmitted long wavelength range stimulates the L-cones, and you see red. (Y + M = R)
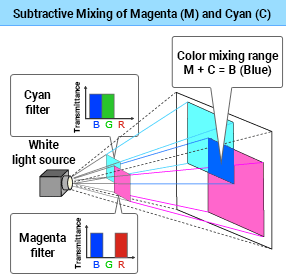
Subtractive Mixing of Magenta (M) and Cyan (C)
The short wavelength range is transmitted by the magenta and cyan filters, stimulating the S-cones, and the brain perceives blue. (M + C = B)
Subtractive Mixing of the Three Primary Color Filters (Y, M, C)
Combining all three primary color filters blocks all the visible wavelengths, resulting in black (K).
As shown above, subtractive color mixing cuts the incident light each time it passes through a filter. (Represented by the size of the arrow in the figure on the right.)
The above explanation assumes that the three primary color filters have the same density. Different filter densities change the color mixing ratio and the resulting color.